ST表,全称 SparseTable,也叫做稀疏表。是用来解决区间和和区间最大最小值问题的一种工具。其实推广开来,其可以用来解决任何可重复贡献(associative)问题。
使用条件
可重复贡献问题
ST表要求其处理的问题必须具有“可重复贡献”这一特征。具体是什么意思呢?
假设有操作F,使得其满足下列关系:
则称F符合可重复贡献问题的特征。
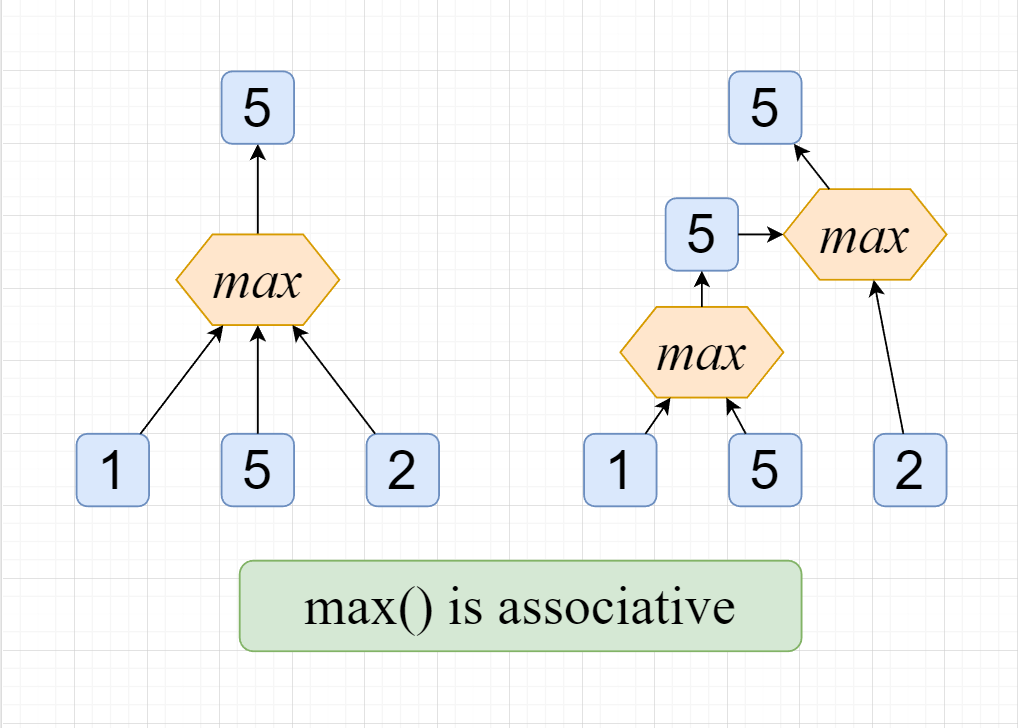
如图,不难发现max()最大值函数就符合可重复贡献问题的特征;读者可以自行验证,sum(),min()等函数都符合这个特征,这也证明了ST表可以解决最大最小值以及区间和等问题。
元数据可不能改变噢
在使用ST表解决问题时,我们必须确保所有的查询结束前,ST表所对应的元数据都不改变。
有些数据结构(比如线段树)在元数据更新之后(比如原来的数组中,某个数值由3变成了5),可以有对应的事件复杂度比较低的方法对结构进行更新,以达到一边更新一边查询的效果。ST表则无法提供类似的方法,所以确保你的问题中没有要求在查询期间动态调整元数据的要求。
SparseTable意义与使用
接下来,我们采用由表及里的过程,先了解ST表的意义以及使用方法,之后再来说明如何生成ST表。
一些准备——向下取整的Log2函数
由于SparseTable的特性,无论是根据数据生成ST表,还是得到ST表后对数据进行查询,都会比较频繁的用到向下取整的log2函数,所以特地说明。我们对于向下取整的log2运算稍加分析,可以得到log2(x)向下取整的具体意义是:
对于某一个数N,返回可能的最大的数字n,使得2的n次方小于等于N,且2的n+1次方必定大于N。
比如对于7,log2(7)向下取整为2,2的2次方不超过7,但可以保证2的3次方一定大于7(8>7)。
了解了这个之后,让我们来看看SparseTable如何快速解决规模庞大的可重复贡献问题吧~
ST表中数据的意义
我们接下来选择一个经典的可重复贡献问题——区间最大值问题,作为示例。
假设我们有一个数组 {3, 2, 1, 4, 5, 9, 7}, 其数据元素个数为7,要求必须在非常低的事件复杂度内,查询某个特定区间(比如从下标0到下标5)的最大值。此时,如果直接循环求解,会导致复杂度随着查询区间长度不断增高,这就是ST表登场的时候啦。
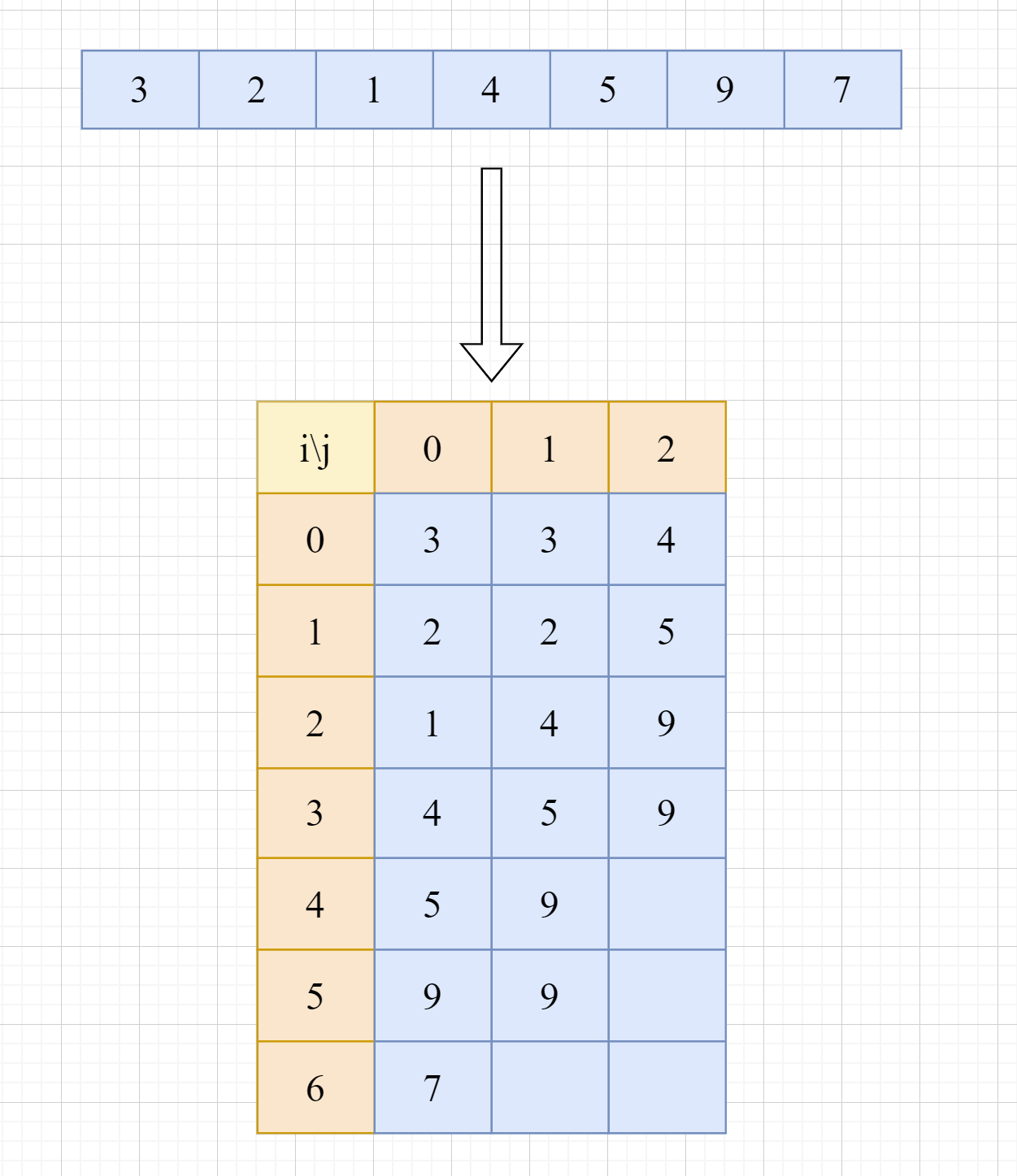
如上图,对数组进行处理之后,就可以得到下方的二维数组,也就是我们大名鼎鼎的SparseTable——ST表。那么问题来了,图中ST表中的数据,到底具有什么含义呢?
首先需要知道的是,ST表正常情况下使用一个二维数组st[idx][pow]来储存。下面对这个二维数组每一个位置元素的意义做出解释:
- 数组中,每一个特定位置
(idx, pow)的值,都代表对应问题在某个区间的解。 - 这个区间的开始坐标为idx。
- 这个区间的长度为2的pow次方。
例如,对于区间最大值问题,假设原数组为arr,处理后得到的ST表中,st[1][2] = 5,则说明:原数组,从下标为1开始,长度为2^2=4的区间内,最大值是5。
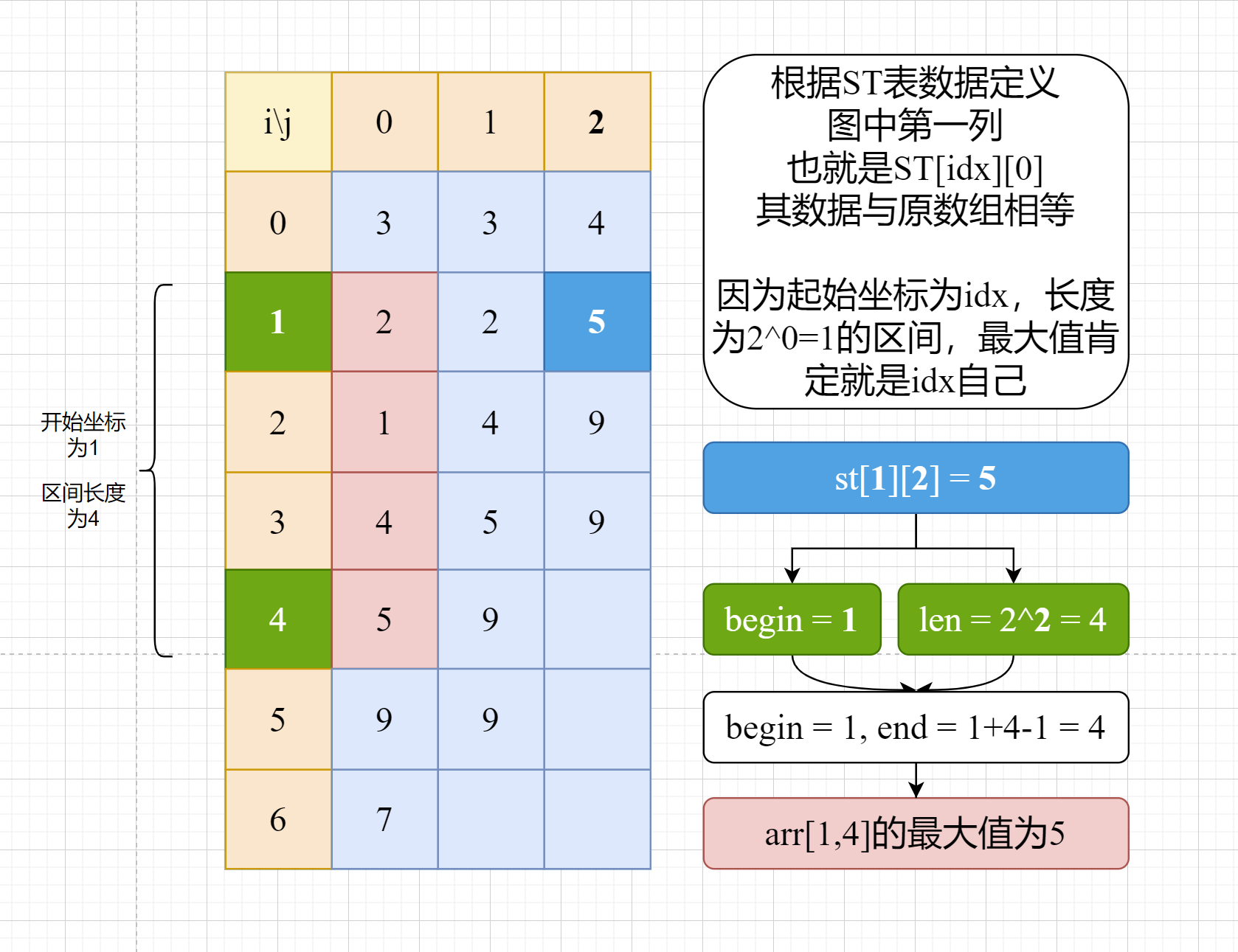
特定区间的查询
知道了ST表的数据的意义,我们就可以着手解决特定区间查询问题。
这里需要注意的是,虽然ST表可以解决不同的可重复贡献问题,但是其在面对不同的可重复贡献问题时,最优查询方式可能有一定的区别。接下来,我们先通过上方的“区间最大值”例子,介绍一下区间最值问题的ST表查询。
合适的长度
首先,为了降低时间复杂度,我们希望用尽可能少的区间查询来拼凑出完整答案。可以证明,在ST表处理区间最值问题时,无论区间长度位置,我们都可以用ST表支持的两个区间,拼接出答案。比如对于区间(1, 6),可以由区间(1, 4)和区间(3, 6)区间的结果再求最值得到。对于“最值”问题,我们只需要保证选择的区间完整覆盖住所求区间,且不超过所求区间即可,而这多个区间允许有重复部分。
同时,为了保证所用区间尽可能少,每个区间就要尽可能大。这个时候,上方说到的log2向下取整计算就派上用场了。由于ST表代表的区间长度只能是2的n次方倍,所以,不超过区间范围的区间,其最长长度就是log(区间长度)向下取整。
比如对于(1,6)区间进行最值计算,log2(6)向下取整=2。说明只需要在合适的位置,用两个长度为2^2=4的区间覆盖即可。这代表了,我们要取的数据肯定在ST[idx][2]内——我们确定了pow。
合适的位置
我们已经知道了,只要位置安排合理,我们肯定能用两个长度为4的区间覆盖住(1, 6),那么这两个区间的位置,应该如何选择呢?
思考之后发现,我们肯定希望:
- 第一个区间尽可能往左,也就是第一个区间的起始下标就是总区间起始下标1。
- 第二个区间尽可能往右,也就是第二个区间的结束下标就是总区间结束下标6。
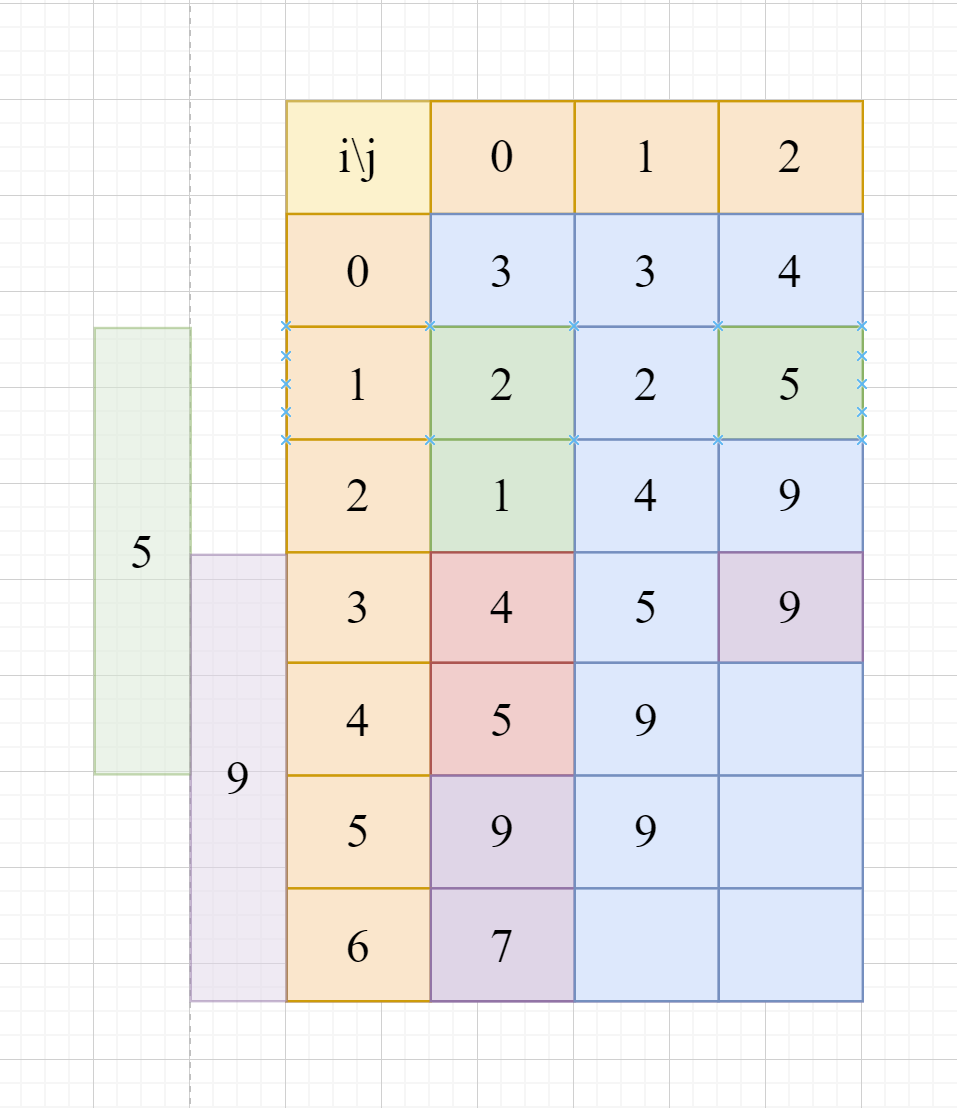
如上图,最终,我们可以得到:
- 第一个区间为(1, 4),最大值为5。
- 第二个区间为(3, 6), 最大值为9。
我们对这两个区间的最大值再求一次最大值即可,最终答案为max(5, 9) = 9。
如果用ST表来计算,运算过程如下:
max(st[1][2], st[3][2])
= max(5, 9)
= 9是时候该自己实现ST表啦
如果您已经掌握了上面所说的,ST表的工作方式,那么恭喜你,欢迎来到ST表的DIY小课堂(bushi),在这里,你将学习如何通过自己的双手书写代码,为一个个数组生成属于他们自己的SparseTable!
初始化
初始值
根据ST表的定义,我们不难得到一个结论,即:
ST表的第一列数据 st[idx][0],与元数据arr[idx]完全相同。
更加准确的说,应该是
st[idx][0] == F(arr[idx]),其中F是本ST表所对应解决的可重复贡献问题。而由于我们以区间最大值为例,所以F(arr[idx]) == arr[idx],最终得到st[idx][0] == arr[idx]。
表的长和宽
解决完初始值,还有另外一个问题,ST表的大小。
我们已经可以确定,表的行数(第一维下标)就是数据个数,比如对于7个数据的数组,生成的ST表肯定有7行。那么一个ST表有多少列呢?
ST表有多少列,取决于查询时最多可能用到第几列的数据。根据ST表的区间查询原理,不难得到,对于数据个数为N的数组,其ST表的最大列数,就是log2(N)向下取整。为什么呢?——因为最坏情况下,需要查询整个区间范围的数据,这时,查询区间长度最大,为N,查询时会调用到的区间的纵坐标(上文的pow),正是log2(N)向下取整。
解决完上面的问题,总算是万事俱备了,我们开始对ST表进行初始化:
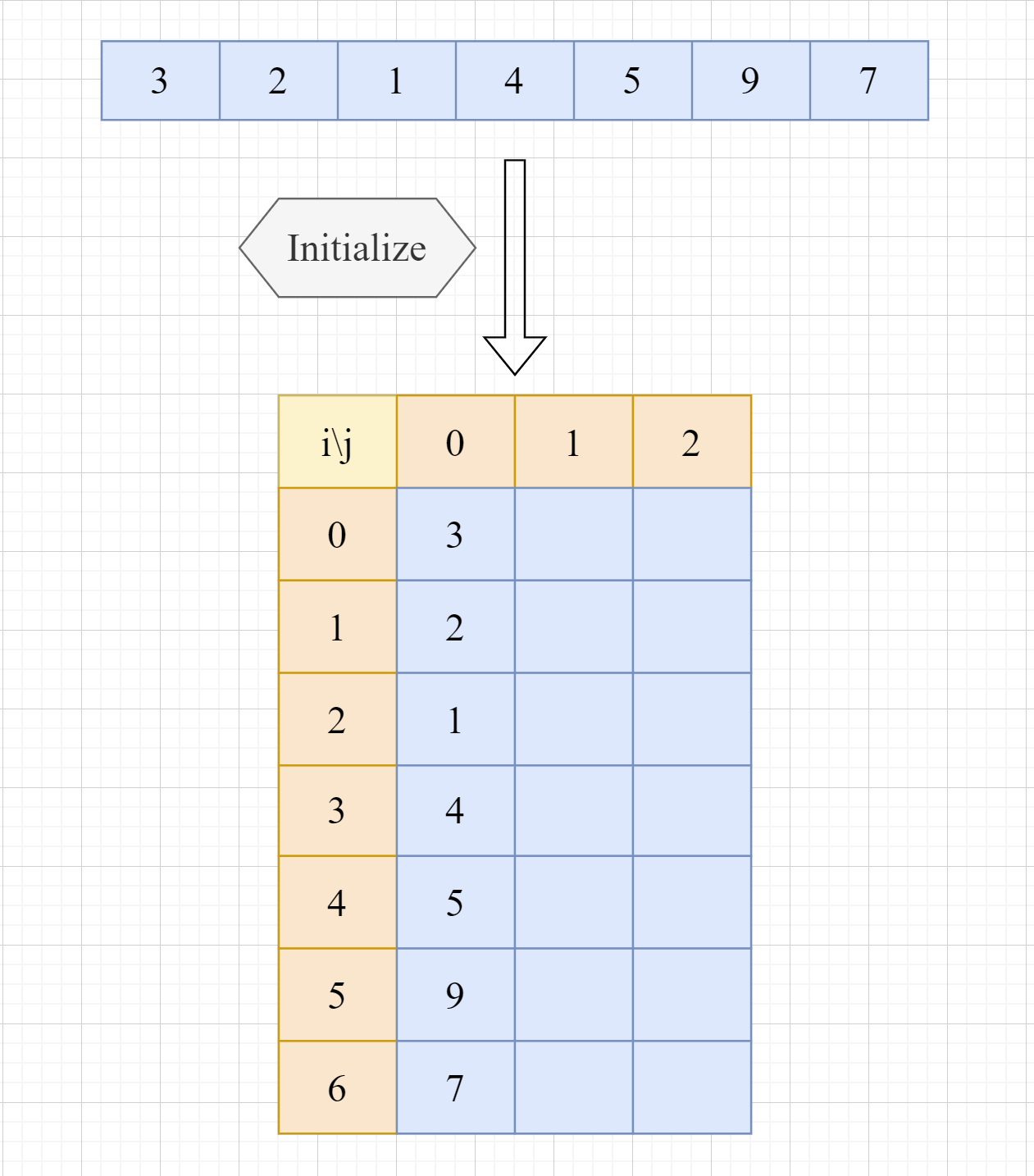
逐步推出整个ST表
接下来的问题便是,如何计算ST表剩余其他部分的值。我们仍然需要从ST表的定义入手,不难发现,由于ST表中的数据本质上就是某个区间的结果,所以更大区间的结果可以由多个小区间结果拼接而来。意思是,我们可以通过表中左边列数据,一步步推出右边的列。(因为左边的列代表范围更小的区间,右边的列代表范围更大的区间,且相邻列的长度差一定是2倍)
由上面的思想启发,我们发现,对于某个位置的ST表st[idx][pow],其左边的ST表列数据已经可用(毕竟我们决定从左边往右边推,那么推到pow列的时候,ST表的pow-1列肯定已经完成计算了),其刚好可以由左边列的两个区间st[idx][pow-1]和st[idx+2^(pow-1)][pow-1]相结合获得。
不要看公式复杂就放弃理解噢~,不难发现,其实其思想与上方”ST表的使用“中所提到的”区间查询“,运用了一样的思想。两个区间都尽可能大,同时一个尽量往左,另一个尽量往右。
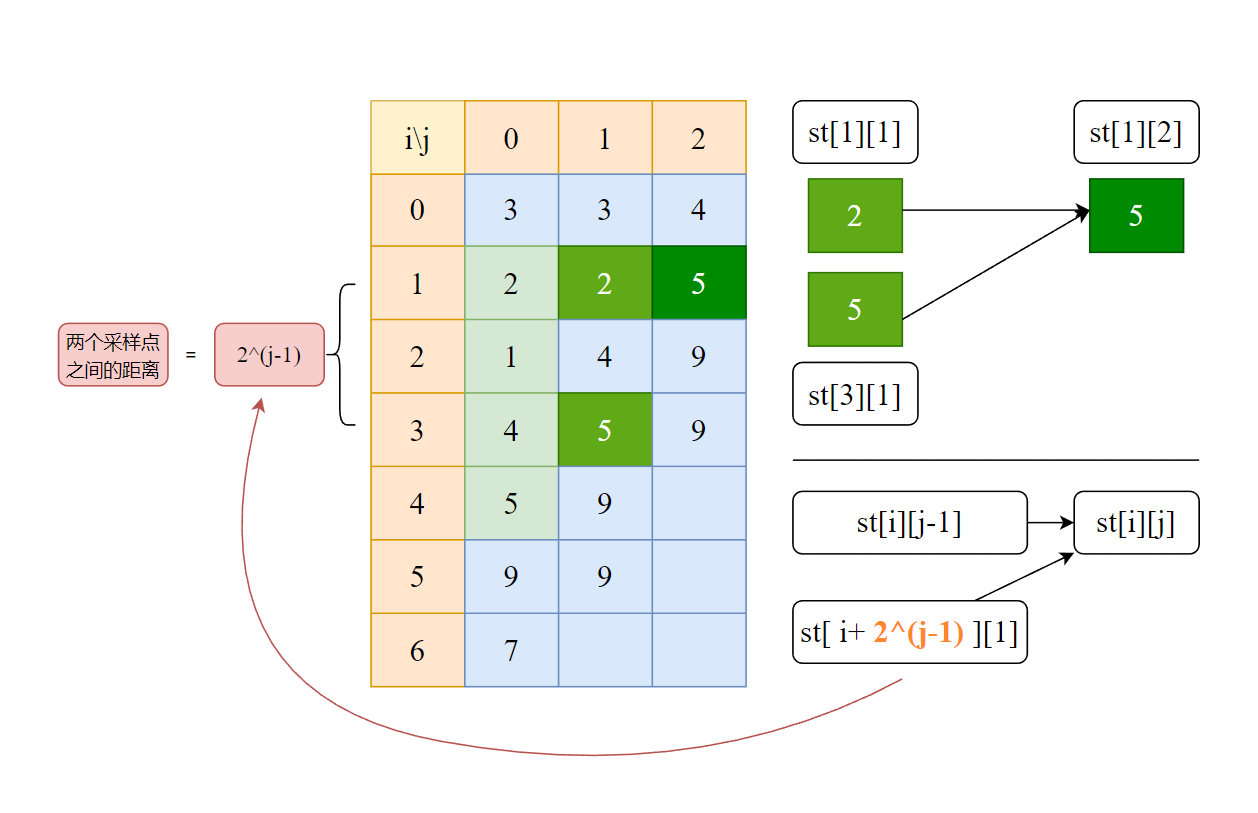
上图就是对某个ST表位置进行求值的示意。知道了某个点的求值方法,我们只需要从上到下,从左往右不停循环,直到求出整个ST表即可。
需要注意,ST表中部分位置没有值,这是因为其对应的区间已经超出范围,比如st[4][2],计算可得,该区间结尾下标为7,但是原始数据个数为7,说明最大下标为6,故该点不应该存在数据,即使存在,查询时也肯定用不到(读者可以自行思考一下,为什么查询的时候不可能调用到这类数据点)。
实战环节!
至此,有关于ST表的所有理论思路都已经介绍完成啦,下面我们借用洛谷上的ST表模板题,来展示一下实际代码:
#include <iostream>
#include <vector>
#include <algorithm>
using LL = int;
using namespace std;
LL st[100000][18] = {0};
LL log2Table[20] = {1};
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = x * 10 + ch - 48;
ch = getchar();
}
return x * f;
}
void initLog2Table()
{
for (int i = 1; i < 20; ++i)
{
log2Table[i] = log2Table[i - 1] * 2;
}
return;
}
LL logLowerBoundTable[100010] = {0};
// 这里实际上是在对上文提到的那个,重要的log2向下取整函数,进行事先缓存,以提高一些查询效率
void initLogLowerBound(const LL &numCnt)
{
logLowerBoundTable[0] = -1;
logLowerBoundTable[1] = 0;
for (LL i = 2; i <= numCnt; ++i)
{
logLowerBoundTable[i] = logLowerBoundTable[i >> 1] + 1;
}
}
int main()
{
// init log2 table
initLog2Table();
// input data
LL numCnt = 0;
LL queryCnt = 0;
numCnt = read();
queryCnt = read();
initLogLowerBound(numCnt);
for (LL i = 0; i < numCnt; ++i)
{
st[i][0] = read();
}
// 这里是在计算,对于数据量N,ST表最多需要的列数是多少
// 上文已经提及
LL maxLayer = logLowerBoundTable[numCnt];
for (LL curLayer = 1; curLayer <= maxLayer; ++curLayer)
{
// LL rightBound = numCnt - log2Table[curLayer];
for (LL curIndex = 0; curIndex <= numCnt - log2Table[curLayer]; ++curIndex)
{
// calculate current arr value
st[curIndex][curLayer] = max(st[curIndex][curLayer - 1], st[curIndex + log2Table[curLayer - 1]][curLayer - 1]);
// cout << st[curIndex][curLayer] << " ";
}
// cout << endl;
}
// deal with query
LL left, right, intervalSize, maxLogNum, maxNum;
for (LL curQuery = 0; curQuery < queryCnt; ++curQuery)
{
left = read();
right = read();
// turn into 0-index
maxLogNum = logLowerBoundTable[right - left + 1];
cout << max(st[left - 1][maxLogNum], st[right - log2Table[maxLogNum]][maxLogNum]) << "\n";
}
}
Little note about this question, that is we must use the accelerated IO method, either like the code above using custom read() function, or add code below into the main() function:
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);